slug plots

I made an (overly) fancy plot for a paper that we decided to not include in the paper, as the biological/clinical (why isn't bioclinical a word? bioinformatics is...) implications are unclear, or uninteresting, or both. Probably both.

The data is about 10 patients with transforming cancers. We have RNA from diagnosis and from transformed disease, which range from a few months to many years down the track. One of the obvious analyses you can do is differential expression. You can do this for each patient separately, or you can group up all diagnosis samples and all transformed samples. Doing the grouped analysis yields a bunch of differentially expressed genes, and some are the usual suspects: MYC et. al. Top tables, volcano plots, etc. All good.

The question we pursued but didn't bother to put in the paper was if this DE signal was related to the time between diagnosis and transformation. We already know that the patients on average have the top DE genes change between timepoints (as they came up as DE), but is the DE signal stronger in some patients than in others. A first approach is to take the the top N genes (default FDR < 0.05 I'd guess...), and check the log fold change for each patient. A signal here would be a correlation between the by-patient mean LFC and time to transformation. It'd be tempting to look at things like average log(p-value) to see how significant the genes are in each patient, but we would then bias by power: we would get stronger signals from less noise or deeper sequenced samples, which we don't care about. Using the uncorrected LFC mostly avoids that confounding factor.


Doing that, we do see a bit of a correlation. Unfortunately, the correlation is driven by variation in the transformed sample (the diagnosis samples don't depend much, if at all, on the transformation time). It's a bit unfortunate, as a correlation on the diagnosis side could in theory be used to predict time to transformation when a patient comes in at diagnosis. If you redo the analysis on more than 10 patients that is, and actually test that the correlation is consistent and reliable over several data sets. As it is, the correlation could be nothing more than the effect of the treatments the patient is undergoing.

Now, after having explained why this isn't in the paper, let's move to the subject of the blog: how would you make a figure out of that?

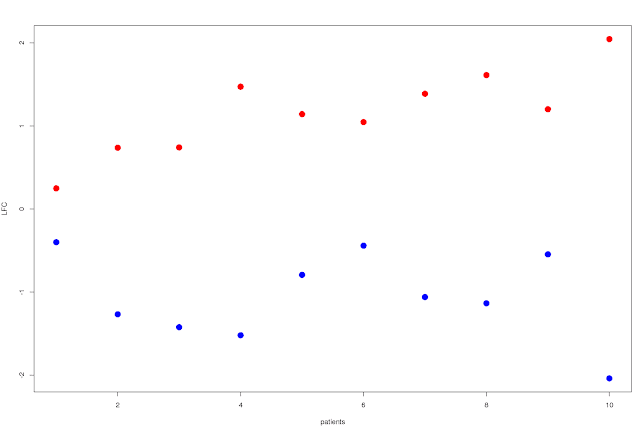
Well, first approach would be to just plot the average LFC by patient over the N significantly up and down regulated (separately ofc) genes, and order the patients by time to transformation. You'd then get a scissors like plot, where the shortest time to transformation have a modest LFC for both up and down regulated genes, and you'd see how they split apart for patients with increasing time to transformation:

This shows that the split increases as you go right on the plot: patients with longer time to relapse has a larger difference in LFC between the top up and down regulated genes. You can probably do something a bit more exciting though, like showing the variance of the LFC in some way... Box plots for example, with standard deviation and percentiles or whatever would already be a lot more useful. It'd look something like this:

The choice of SD and quantiles are a bit arbitrary of course, and if we want to go the full stretch and show the complete distribution of the LFCs of the top N genes we can always go to violin plots, that are essentially sideways smoothed histograms:

Well, that's the end of that I guess. Or is it?? This blog wouldn't be here if it were, so anyone familiar with the anthropic principle (with the universe replaced by this blog) will realise that there is another step. Also you can see on the scroll bar that there is still some left of the blog. You also haven't seen the plot that was used to advertise the blog (unless you've scrolled down, which you probably have), which is kindof a tell. Anyway, onwards.

Do the most DE genes in the group comparison separate the patients better? Is it better to go down to FDR < 0.5 to get more genes and more power? No reviewer would object to the choice of FDR < 0.05, or even think of it twice, but that doesn't change the fact that the cut-off is very arbitrary.

We can get rid of it if we don't plot just a subset, but we plot the ranking. That is, we plot the violin plot for the top N genes in red/blue, Inside that we plot the top N/2 genes with half width in orange/cyan. And so on. All on top of each other. With just two overlapping violins, you get this:

This shows a bit more information, but it's also messy. Let's start by doing two half-violins for the up and down regulated gene sets. Then do the above violins-inside-violins, but put a gradient from black to red to yellow to white for the upregulated genes, and black to blue to cyan to white for the downregulated genes. So make a continuous number of violins (well, in the computer it'll always be discreet, but small enough steps to look continuous). So the red colour shows the distribution of the largest gene set, and as we strip down the gene set to only the very top ranked genes, the colours shift to brighter colours. You then get this:

It kindof looks like slugs slugging their way up and down a wall, doesn't it? Imagine frames of a stop-motion of a slug movie. The blue slug going down, the red going up. So well, I'm calling them slug plots. :)

At the end of the day, this is a pretty plot more than a useful plot. Yes, it contains a lot of information in the sense that it shows the distribution for any top N genes, but it is not really immediately obvious if you are looking at a significant signal or not. It is not clear where the magical FDR = 5% limit is. You do however see that the higher ranked genes have a stronger signal (the white parts of the slugs climb up higher than the red parts), which is neat.

Anyway, maybe there is a use for someone. Essentially it can be used when you have several DE contrasts you want to compare to a ranked gene list (potentially from another DE contrastt). If you want to make your own slug plots, there is an R package called slugPlot now. :)

library(devtools)
install_github('ChristofferFlensburg/slugPlot')
library(slugPlot)
example('slugPlot')
?slugPlot

It is all a bit thrown together, so feel free to improve or add things if you want.

Frequency scatters in superFreq

SuperFreq is a cancer exome analysis pipeline developed in my lab, handling SNVs, CNAs and clonal tracking. This blog goes a bit more in depth of why and how we constructed one of the plots in superFreq, and how you can make the most of it.

I will talk about the variant frequency scatter plot. The idea behind this plot is to show the data in a relatively unprocessed way, to make it easier to understand and quality control the data. I often use these plots to verify that signals in the analysis are real. You can also use it for discovery to some extent, but it is not the main purpose. The plot is simply a scatter plot of the variant frequencies in two samples from the same individual. All variant provided in the input .vcf are shown in the default plot. If you plot only that, you get a plot like this:

As example, I will show a follicular lymphoma sample that transformed into large diffuse B-cell lymphoma. The frequency of the SNVs in the first time point is on the x-axis, and the frequencies of the SNVs in the transformed disease is on the y-axis. This is not a whole exome, but sequencing over exons of a panel of around 700 genes. I use this as example to make the plots less cluttered as we walk through the steps, but I will show a whole exome further down.

This plot above, to be frank, isn't very useful. Only thing we can say from here is that there are a lot of variants, and we see clusters around (0,0), (0.5,0.5) and (1,1). The absence of clusters at (0,1) and (1,0) tells us that the samples probably are from the same individual, ie correctly matched samples, but hard to say much more.

Point size by accuracy

The first improvement to the plot is the usual point size by accuracy. Here, the error of the frequency scales inversely with the square root of coverage, so the inverse of that (ie, the square root of the coverage) seems like a reasonable size of the points. This also makes the area of the points proportional to the coverage, which is a nice property. The total area of the points in a cluster describes the total number of reads that supports the cluster. Cool! There are more details in this, such as the geometric mean of the coverage between the two samples (we want a variant with low coverage only one sample to show up as small) and the cut-off for small (let's show at least a tiny dot) and large (once a dot is pretty accurate we don't care enough to clutter up the plot) dots, but let's not get into too much details.

Point size by accuracy. Area of dots proportional to read depth.

This defines the (0.5,0.5) cluster a lot more, and most of the points outside the main clusters turn out to just be low coverage variants, with high uncertainty in the frequency. Probably nothing to get excited about. There a few large point well outside the main clusters though. And maybe a few of them even seem to cluster up a bit? Hmm...

Grey low quality variants

Next, let's go QC the variants. SuperFreq checks the .bam of each file, looking for poor mapping or base quality. Chances are that the caller you used to produce the .vcf already did something similar, but just in case... SuperFreq also cross-checks the variants against a set of reference normal samples, and flags variants that behaves suspiciously in the normal ("suspicious" in this context amounts to be present, with some leeway given to potential population variants around 50% or 100% frequency). Let's replace the flagged variants with grey rings, and put then in the background:

Flagged variants are shows as grey rings.

Well, most variants seem to pass the filters. Mainly the low frequency variants around (0.1,0.1) are affected. This tempts us to believe that the rest of the low frequency variants (at (0.05,0.05)) probably also are not real, or at the very least not reliable enough to take seriously. Probably the lower frequency goes for the reference normals as well, and the variants slipped below the noise-level cuts.

crosses for dbSNP

The (0.5,0.5) and (1,1) clusters are likely the germline heterozygous and homozygous variants, so they should be enriched for common population variants. Let's cross-check with dbSNP and replace population variants with black crosses instead of blue dots.

dbSNP variants shown as black crosses, or grey crosses if flagged.

What a difference! The (0.5, 0.5) and (1,1) clusters are mainly dbSNP variants, as expected! The clusters at (0.45, 0.1) and (0.55,0.9) seem to also be dbSNP variants. There are a few non-dbSNP variants in the (0.5,0.5) cluster, a large fraction of the (0.05, 0.05) noise SNVs are also non-dbSNP, There is a non-dbSNP cluster around (0.1, 0.4).

This information gives us quite some power to tell what the cluster are.The non-dbSNP clusters are probably not germline variant, and thus either noise or somatic SNVs. It is fair to assume that the low frequency variants are mostly noise, as they cluster with the flagged grey variants. The (01, 0.4) non-dbSNP variants is probably the most interesting one, as it likely is somatic variants. They are high frequency in one sample, and low in the other, making it unlikely to be noise. Being a blood cancer that typically is mostly diploid, these frequencies correspond to clonalities of 0.2 and 0.8 in the two samples. So these SNVs were present to low degree at the first timepoint and then dominates the relapse. This is where we will find the mutations that are causing the disease transformation.

There is then a pair of dbSNP clusters at (0.45, 0.1) and (0.55, 0.9) that is probably related to a copy number loss. We already suspect that there is a population of cell at ~20% clonality in the first sample and 80% in the second, and a loss in these cells would give this signal: the lost heterozygous germline SNPs would shift down to around 40-45% in the first sample, and to around 10% in the second, and we would have the mirror image for the retained heterozygous germline SNPs. The fact that these are mostly dbSNPs leads us to this conclusion. If we find a cluster of mostly non-dbSNP at (0.45, 0.1) we would assume it is somatic SNVs, so the dots vs crosses allows us to separate these two kinds of clusters.

colour by significantly different frequency

In general, things along the x=y diagonal are less interesting, and we want to know if clusters are significantly separated from the diagonal. To do this, we run a fisher exact test (reference and variant counts in both samples) to check for significant difference in frequency between the samples. Add in a multiple hypothesis correction, and colour the dots or crosses red as they approach global significance. We set the limit so that a null set (replicate samples, expecting only x=y) will have a couple of dots turning a deep red, so that a shiny red dot or cross usually means significant signal.

Colour red if significantly different frequency in the two samples.

We see that the three clusters we talked about are indeed significantly off-diagonal. Essentially this is just a bit of a confirmation that we didn't imagine the clusters, and it helps draw the eye to them when we look at the plot the first time.

gene names

We now want to figure out a bit more what the new somatic SNVs are, as they can be biologically relevant. For this, let's add gene names over all SNVs that are sufficiently red.

Add gene names over red dots or crosses.

We get four gene names in the somatic SNV cluster, which are candidates for playing a role in transformation. We also note that some of the genes in the dbSNP clusters have SNPs in both the upper and lower cluster, which confirms that the two clusters are associated with each other. If we want to, we can go and check up which chromosomes FRK, TTK and EPHA7 are on, and it'll turn out that they are all on the chr6q arm. For copy number calls, probably better to look at the copy number plots otherwise, which are described in the manual on github (link on top).

Highlight protein changing SNVs

Finally, we want to know if the somatic SNVs damage the protein of their gene. Running the somatic variants through VEP, we mark the protein altering SNVs with an orange border (thicker border for more severe, such as nonsense or frameshift mutations).

Add rings around protein changing somatic SNVs.

We see now that CCND3 is the only one of the names somatic SNVs that is actually protein altering, making it a prime candidate for causing the relapse. Going to the literature, you can find support for CCND3 playing a role in transforming blood cancers, which is encouraging.

Whole exome example

The above plots are from an older version of superFreq, and on the a capture set of only around 700 of the 20k genes. By now, superFreq also highlights protein changing SNVs that in the cosmic census of cancer related genes. A typical (blood cancer, so mostly diploid) scatter between two cancer timepoint with whole exomes will look something like this (showing the version without gene names for less clutter). You can see how it grows out of the raw scatter in this animation:

Animation of gradual introduction of the steps explained above (plus the COSMIC highlighting) in a scatter plot between two different time points of a blood cancer. The title of the plot shows the step currently being introduced.

The final version looks like this in a bit higher resolution.

A typical scatter between two different time points in a blood cancer. The green rings highlight somatic protein changing SNVs in COSMIC census genes.

 I'm leaving the interpretation of this plot to the reader as an exercise. How many clusters can you find, and what do they mean? There are at least 11 clusters. Post in comments or on twitter or whatever media may have lead you to read this. :)

As closing remark, let me say that while it is possible to read a lot of information from these scatters, many of them can more conveniently be read from other output in superFreq. The big strength of the scatters is that they show the data in a comparably raw and unprocessed manner. You don't just get the CNA calls, or just a top table of somatic SNVs according to some frequency cuts. Looking at this plot it is often easy to convince yourself if you are looking at a real signal or noise, which can be hard in more processed downstream results. So before you publish anything, check in the scatters that the signal actually look reasonable. ;)

This concludes the first blog on superFreq. I'll try to keep it up, and explain different parts of the pipeline, both what is going on underneath the hood, and how you can interpret the output. I'm open for requests if you are curious on some specific part. More details are in the manual on github (linked on top). Thanks for reading!